Tool Chain: UML2oWFN and LoLA
Behavioral Analysis of UML2 Activity Diagrams (IBM WebSphere Business Modeler process models) with LoLA. We describe how to combine our UML-to-Petri Nets compiler UML2oWFN and our model checker LoLA: A Low Level Petri Net Analyzer in a tool chain for verifying soundness of processes modeled in IBM WebSphere Business Modeler.
Getting the input data
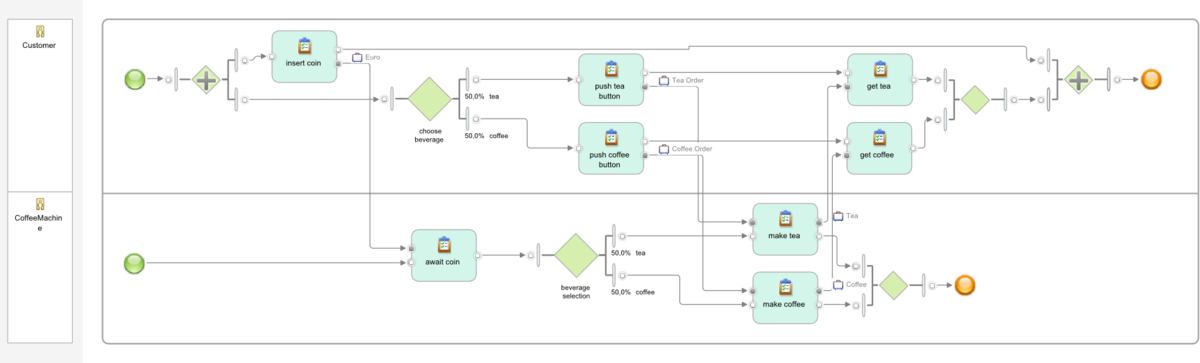
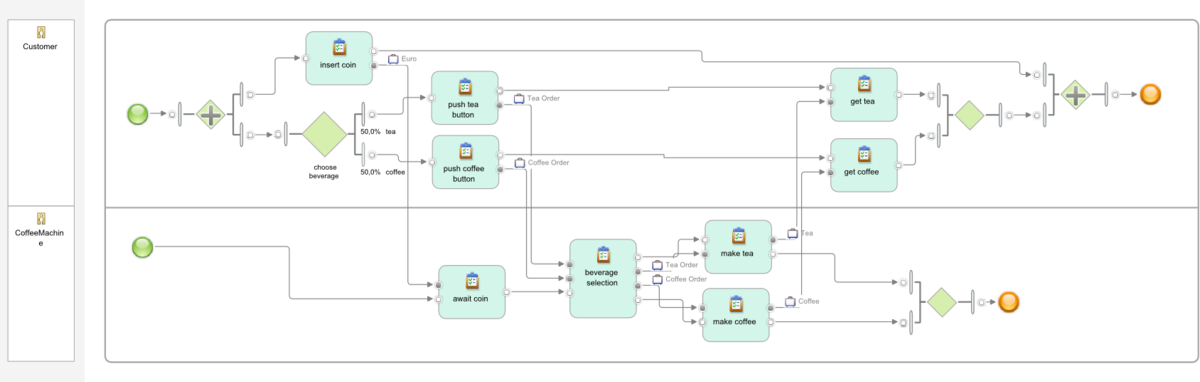
Our example is the process model of a coffee machine and its interaction with a customer. You can download the process model in IBM WebSphere Business Modeler .xml format here (file service-tech.xml). The model contains the following two, almost identical, processes.
You can re-import service-tech.xml into your IBM WebSphere Business Modeler if you want to, our tools will work directly on the .xml file.
Getting the tools
We now give a brief walk-through for setting up UML2oWFN and LoLA for this tool chain. A detailed explanation for installation and use of both tools is available on the respective pages.
1. Create a directory for setting up the tool chain, e.g.
mkdir uml-analysis
cd uml-analysis
2. Download lola-1.15.tar.gz into uml-analysis/, then unpack, rename, and configure LoLA as follows
tar xzf lola-1.15.tar.gz
mv lola-1.15 lola
cd lola
./configure
cd ..
LoLA is now prepared to be used with UML2oWFN.
3. Download uml2owfn-2.00.tar.gz into uml-analysis/, then unpack, renaming is optional, configure and compile UML2oWFN as follows.
tar xzf uml2owfn-2.00.tar.gz
mv uml2owfn-2.00 uml2owfn
cd uml2owfn
./configure
make
cd ..
The make call in uml-analysis/uml2owfn/ will also invoke make for LoLA in uml-analysis/lola/ to build four dedicated LoLA binaries that are needed for analyzing processes. If everything was setup correctly, you will find files lola-sp, lola-mc, lola-lp, and lola-full-limited in uml-analysis/uml2owfn/lola/. When building under Cygwin, these files will have the .exe extension.
4. Make all created binaries available on the command-line for your analysis. For this example, we propose to set up an analysis directory uml-analysis/coffeeMachine/ as follows.
mkdir coffeeMachine
cp uml2owfn/src/uml2owfn coffeeMachine/
cp uml2owfn/lola/lola-* coffeeMachine/
cd coffeeMachine
Under Cygwin, you will have to add the .exe extension for the cp comand. Now the tool chain is ready for use. Download the example file service-tech.xml to uml-analysis/coffeeMachine/ to begin with the analysis.
Translating processes to Petri nets
This tool chain begins with translating the original process model into Petri nets with UML2oWFN. Invoke the following command:
./uml2owfn -i service-tech.xml -f lola -a soundness -a safe -a orJoin -p ctl -o
You will get a line saying 2 of 2 processes have been translated. and you will see 6 new files
service-tech.Prcsss__coffeeMachine_sound
service-tech.Prcsss__coffeeMachine_unsound
with extensions .lola, .lola.fin.task, .lola.safe.task. The .lola files are Petri nets that have the same behavior as the original process models, the .task files describe correctness properties these nets have to fulfill.
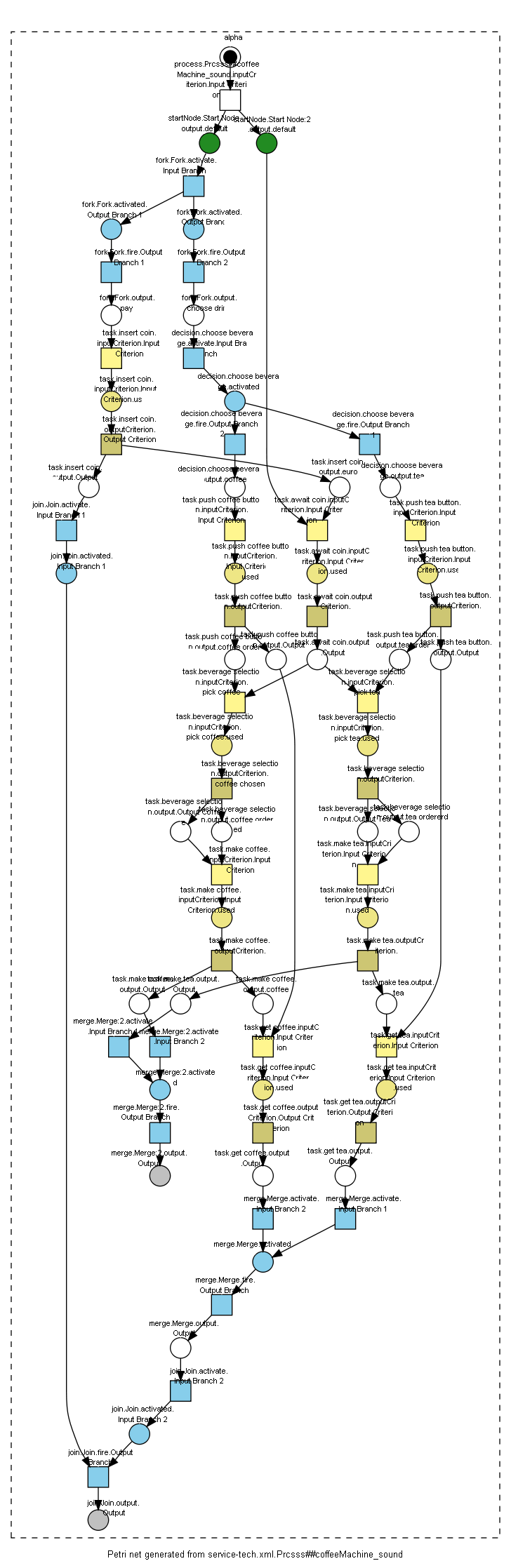
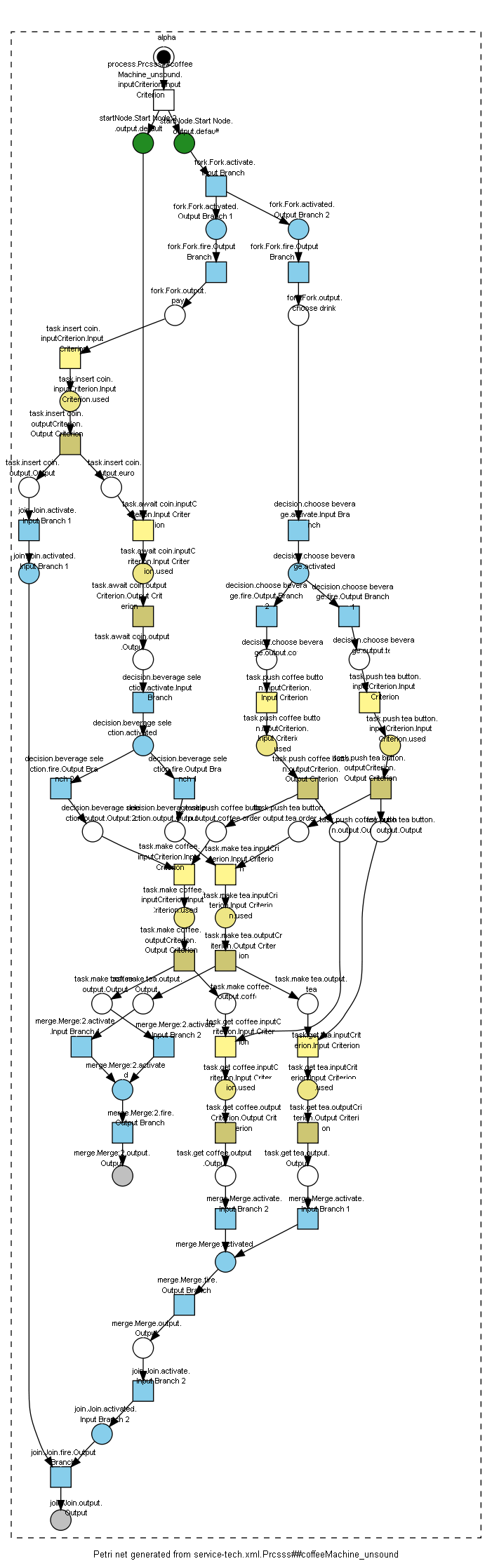
If you want to inspect the Petri nets, you can either use our editor Seda or use UML2oWFN to generate a .png file that shows the Petri net (this requires GraphViz dot to be available on your system). Invoke
./uml2owfn -i service-tech.xml -f dot -a soundness -a safe -a orJoin -o
to get the two graphical representations of the processes as shown on the right.
There are more output formats available, see the Manual for details.
Analyzing the generated Petri nets
In the last step, we generated files that are a compatible input for LoLA. The .lola files describe a Petri net in LoLA syntax. The .task files describe behavioral properties of the net.
The .lola.fin.task describes that the process must always be able to reach a valid final state, i.e. that it has no deadlock. The .lola.safe.task describes that the process must not reach a state that allows him to execute the same task twice, i.e. that the process has no lack of synchronization. In Petri net terms, we require that no place of the net may have more than one token, i.e., that the Petri net is safe. Both properties are checked separately by LoLA with dedicated routines.
To check all of these properties for all of the nets, invoke
sh ./check_service-tech.sh ./ &> ./results_service-tech.log
which will call for each process and each property the respective LoLA binaries. Note the parameter ./ to the shell script which points to the location of the LoLA binaries.
All output is written to the file ./results_service-tech.log. From there, analysis results can be parsed and interpreted. We now explain in detail how LoLA is invoked for each analysis and how the analysis results are interpreted. A method for automatically running this tool chain with translation, analysis and result interpretation is explained in the UML2oWFN manual.
Details on the analysis of the generated Petri nets
Analyzing deadlock freedom
To verify that a process can always terminate, we use lola-lp.
Verify coffeeMachine_sound.lola
Call
./lola-mc service-tech.Prcsss__coffeeMachine_sound.lola \
-aservice-tech.Prcsss__coffeeMachine_sound.lola.fin.task -P
to verify the first coffee machine process. (Note that between parameter switch -a and the subsequent file name is no space.) As a result you will get the following print out
44 Places
36 Transitions
35 significant places
Formula with 48 subformulas and 2 temporal operators.
result: true
>>>>> 159 States, 475 Edges, 159 Hash table entries
NO PATH
The line result: true tells us that the process indeed can always reach a valid final state.
Verify coffeeMachine_unsound.lola
If you verify the second coffee machine process with
./lola-mc service-tech.Prcsss__coffeeMachine_unsound.lola \
-aservice-tech.Prcsss__coffeeMachine_unsound.lola.fin.task -P
then you will get
41 Places
35 Transitions
34 significant places
Formula with 45 subformulas and 2 temporal operators.
result: false
>>>>> 44 States, 55 Edges, 44 Hash table entries
PATH
process.Prcsss##coffeeMachine_unsound.inputCriterion.Input_Criterion
fork.Fork.activate.Input_Branch_
fork.Fork.fire.Output_Branch_1
fork.Fork.fire.Output_Branch_2
task.insert_coin.inputCriterion.Input_Criterion
task.insert_coin.outputCriterion.Output_Criterion
task.await_coin.inputCriterion.Input_Criterion
task.await_coin.outputCriterion.Output_Criterion
decision.beverage_selection.activate.Input_Branch_
decision.beverage_selection.fire.Output_Branch_2
decision.choose_beverage.activate.Input_Branch_
decision.choose_beverage.fire.Output_Branch_1
which tells that the process is not sound and provides an error trace in the Petri net to a state from which on it is impossible to reach a valid final state.
Analyzing lack of synchronization (safeness)
To verify that a process has no lack of synchronization, we use lola-sp. Call
./lola-sp service-tech.Prcsss__coffeeMachine_sound.lola \
-aservice-tech.Prcsss__coffeeMachine_sound.lola.sound.task -P
The resulting print out should read like this.
44 Places
36 Transitions
35 significant places
Formula with 3 subformula.
predicate is not satisfiable!
>>>>> 42 States, 48 Edges, 42 Hash table entries
The line predicate is not satisfiable! tells us that the process has no lack of synchronization as LoLA tries to find a state that witnesses the violation of that property. You will get the same result for the unsound coffee machine.
Understanding the analysis results
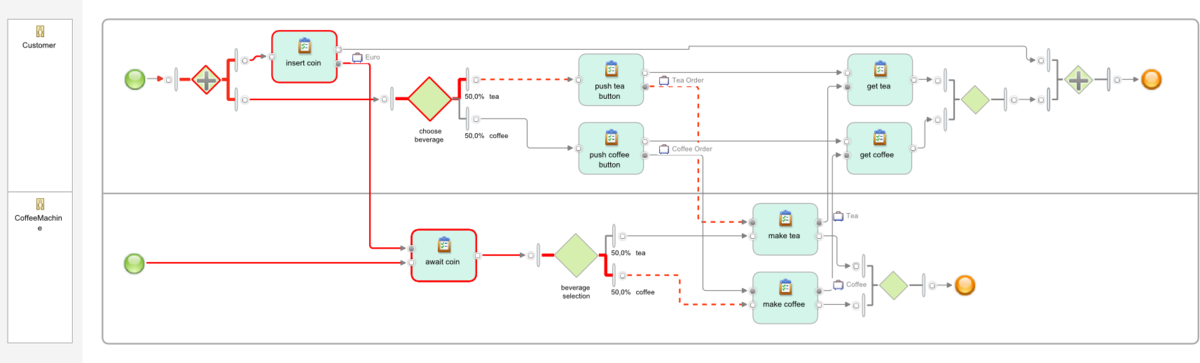
The error trace which we obtained in the the deadlock verification can be mapped back to the original model based on the Petri net transitions mentioned in the trace and their originating tasks in the original process model. This mapping has to be done manually; the following figure illustrates the above error trace (only solid red lines) in the original model.
The error occurs because the coffee machine can choose independently of the customer which beverage it produces. If the choices do not match, the process deadlocks.
The problem can be solved by replacing the independent XOR-choice of the coffee machine by a choice that depends on the input from the customer. In UML, this requires using input pinsets and output pinsets on the choosing task. This has been done in the sound coffee machine for task beverage selection as follows:
input tea order and the control-flow link activate the output tea order and the upper control-flow link
input coffee order and the control-flow link activate the output coffee order and the lower control-flow link.
This yields the Petri net pattern on the right. With this process logic, the coffee machine process is sound.